
Sobolev Spaces on Metric Measure Spaces
1 502 kr
1 502 kr
På lager
To., 6 feb. - on., 12 feb.
Sikker betaling
14 dagers åpent kjøp
Selges og leveres av
Adlibris
Produktbeskrivelse
Analysis on metric spaces emerged in the 1990s as an independent research field providing a unified treatment of first-order analysis in diverse and potentially nonsmooth settings. Based on the fundamental concept of upper gradient, the notion of a Sobolev function was formulated in the setting of metric measure spaces supporting a Poincaré inequality. This coherent treatment from first principles is an ideal introduction to the subject for graduate students and a useful reference for experts. It presents the foundations of the theory of such first-order Sobolev spaces, then explores geometric implications of the critical Poincaré inequality, and indicates numerous examples of spaces satisfying this axiom. A distinguishing feature of the book is its focus on vector-valued Sobolev spaces. The final chapters include proofs of several landmark theorems, including Cheeger's stability theorem for Poincaré inequalities under Gromov–Hausdorff convergence, and the Keith–Zhong self-improvement theorem for Poincaré inequalities.
Artikkel nr.
ec0cb7ef-c4cf-4f33-a6ea-b7fd80999c48
Sobolev Spaces on Metric Measure Spaces
1 502 kr
1 502 kr
På lager
To., 6 feb. - on., 12 feb.
Sikker betaling
14 dagers åpent kjøp
Selges og leveres av
Adlibris
Lignende toppselgere

Generic
Øreputer for Bose QuietComfort - QC35/QC25/QC15/AE2 Hodetelefoner Svart
99 kr
4,5(712)
mandag, 27 jan.

INF
Universallader for Garmin klokker
90 kr
4,3(262)
fredag, 24 jan.

CherrysC
Squid Game 2 Gonggi & Case Korean
129 kr
fredag, 31 jan.

Odin
Titan Silikon Til Tredemølle 100ml
149 kr
Tidligere laveste pris:
349 kr
5,0(5)
fredag, 24 jan.

INF
INF Sklisikker beskyttelse / brodder for sko med 18 stålpigger (L)
259 kr
Tidligere laveste pris:
291 kr
4,4(22)
torsdag, 23 jan.

Maaleo
Dobbeltsidige tusjer/penner - 168 stk. MAALEO 24101
399 kr
3,0(2)
torsdag, 6 feb.

Megabilligt
Galaxy Lamp - Nebula Star -projektoren med fjernkontroll
499 kr
Tidligere laveste pris:
909 kr
3,8(28)
mandag, 27 jan.

Brädspel.se
Spill Kluster (SE/FI/NO/DK)
321 kr
4,9(8)
tirsdag, 28 jan.

Seven Steelbook (4K Ultra HD + Blu-ray)
349 kr
fredag, 24 jan.

PlayStation 5 Slim Digital Edition (PS5)
5 789 kr
4,4(38)
fredag, 24 jan.
Anbefalinger til dig

Generic
RCA til HDMI Converter 1080p - Adapter
129 kr
4,4(15)
mandag, 27 jan.

Generic
2-Pak - PS4 Kontroll DoubleShock for Playstation 4 - Trådløs
549 kr
4,1(9)
mandag, 27 jan.
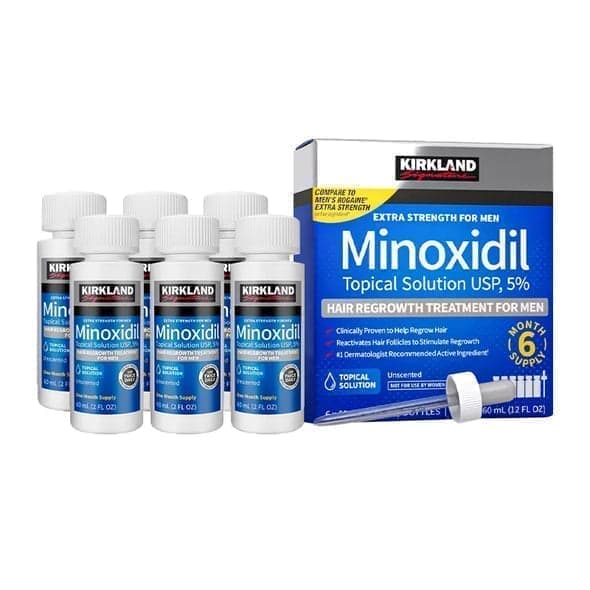
KIRKLAND
6x60ml = 360ml - Kirkland Extra Strength 5% Men Hair Regrowth 60ml Hair Loss
1 290 kr
5,0(5)
fredag, 24 jan.

INF
INF Tilbehør Roborock S6/S60/S65/S5 Max/T6, 20 deler
386 kr
3,3(25)
torsdag, 23 jan.

Mobil o Teknik
Elektrisk babyneglefil - fra nyfødt til småbarn
199 kr
4,0(5)
tirsdag, 28 jan.

Generic
2-Pak - iPhone Lader Adapter+Kabel 20W USB-C Hurtiglader
199 kr
3,7(503)
mandag, 27 jan.

INF
INF Stylus Pen kompatibel med iPad 2018-2023-serien HvitiPad
269 kr
4,1(43)
fredag, 24 jan.

Pro
Digital vekt - lommevekt, smykkevekt 0,01 - 200g
119 kr
4,2(25)
onsdag, 22 jan.

Megabilligt
Sovende hodetelefoner - Hodebånd og øyemaske med Bluetooth -hodetelefoner
249 kr
Tidligere laveste pris:
299 kr
3,9(20)
mandag, 27 jan.

INF
INF Tilbehør til Roborock S5/S6 modeller 7 deler
219 kr
4,2(49)
torsdag, 23 jan.